[Algorithm] LIS(Longest Increasing Subsequence)
CONCEPT
LIS는 Longest Increasing Subsequence의 약자로 ‘최장 증가수열’, 또는 ‘최대 증가 부분수열’로 불린다. LIS는 어떤 수열에서 특정 부분을 지워서 만들어낼 수 있는 증가 부분수열(Increasing subseqence)중 가장 긴 수열을 말하는데 이때 부분 수열의 숫자들은 원 배열에서 위치가 이어져 있지 않아도 된다는 특징이 있다.
LIS를 구하는 방법은 가장 대표적으로 3가지 방법이 있다.
완전탐색 방법
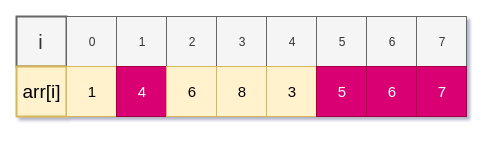
가장 직관적이고 쉽게 생각해 볼 수 있는 방법은 완전탐색을 이용한 LIS 방법이다. 아래의 배열을 예시로 들어보자.

i가 0부터 6일때까지 차례대로 완전탐색을 통해 LIS을 구할 수 있다. 코드를 확인해보자
완전탐색(code)
int LIS[8][8];
int size[8];
int MAX = -1;
int lis_size;
for (int i = 0; i <= 7; i++) {
LIS[i][0] = arr[i];
size[i]++;
for (int j = i + 1; j <= 7; j++) {
if (arr[j] > LIS[size[i]]) {
LIS[++size[i]] = arr[j];
}
}
}
for (int i = 0; i <= 7; i++) {
if (MAX < size[i])
MAX = size[i];
}
lis_size = MAX;
이렇게 구한 LIS에서 몇 가지 특징을 유추할 수 있다.
위 부분 증가수열은 [4, 5, 6, 7]인데, 이 부분수열을 S라고 할 때,
-
정수 i, j에 대해 i<j이면, S[i] < S[j]다. (0 <= i, j<= S ) -
정수 i, j에 대해 S[i] < S[j]이면, 원 배열 arr에서의 S[i], S[j] 두 수의 위치 전후관계는 같다. (0<=i, j<= S )
다이나믹 프로그래밍(DP)
DP를 이용한 LIS를 구하는 방법은 이렇다. 아래의 코드에서 length_dp[i]는 i번째 인덱스에서 끝나는 최장 증가 부분수열의 길이를 의미한다.
for (int i = 0; i < n; i++) {
length_dp[i] = 1;
for (int k = 0; k < i; k++) {
if (arr[k] < arr[i]) {
length_dp[i] = max(length_dp[i], length_dp[k] + 1);
}
}
}
주어진 배열에서 인텍스를 한 칸씩(i+=1) 늘려가면서 확인한다. 그리고 내부 반복문으로 i 보다 작은 인덱스들을 하나씩 확인해나가며 arr[k]<arr[i]인 것이 있을 경우, length_dp[i]를 업데이트한다.
업데이트하는 기준은
- k번째 인덱스에서 끝나는 최장 증가 부분수열의 마지막에 arr[i]를 추가했을 때의 LIS의 길이
- 추가하지 않고 기존의 length_dp[i] 값
둘 중에 더 큰 값으로 length_dp[i] 값을 업데이트한다.
이분탐색
완전탐색과 DP를 이용한 LIS는 시간복잡도의 문제가 발생할 수 있는데, 이를 개선하기 위한 방법으로 이분탐색을 활용한다.
이때 LIS의 형태를 유지하기 위해 주어진 배열의 인덱스를 하나씩 살펴보면서 그 숫자가 들어갈 위치를 이분탐색으로 탐색해서 넣는 방법을 사용한다. 여기서 숫자가 들어갈 위치를 판단하는 기준은 정렬된 배열에서 찾고자 하는 값 이상이 처음으로 나타나는 위치인 Lower Bound의 개념을 이용한다.

Lower Bound 개념을 이분탐색 알고리즘에 적용하여 구현할 때 lis[] 배열을 사용하자.
여기서 lis[i]는 (i+1)의 길이를 갖는 최대증가수열을 만들때, 가능한 가장 작은 수를 의미한다.
int lis_lowerbound(int n){
int i,j;
int len = 0; // 현재 lis 배열의 마지막 원소 인덱스
lis[0] = arr[0];
for(i=1;i<n;i++){
len = len + lower_bound(arr[i],len);
}
return len+1;
}
int lower_bound(int target, int len){ // 자신보다 큰 값들 중 가장 작은 값의 인덱스 리턴
int start,end,mid;
start = 0;
end = len;
if(target > lis[end]){
lis[len+1] = target;
return 1; // lis 배열에 새로 추가되었을때(최대증가수열의 값이 증가하였을때)만 1을 리턴해서 최종길이를 1씩 늘려준다
}
while(1){
if(end-start == 1){ // 이분탐색중 두개의 원소만 남았을때
if(lis[start] < target){
lis[end] = target;
}
else{
lis[start] = target;
}
return 0; // 기존의 값이 대체된것이므로 0을 리턴해서 최대길이를 늘리지않는다
}
if(end == start){ // lis의 원소가 1개일때
if(lis[end] > target){
lis[end] = target;
return 0; // 기존의 값이 대체된것이므로 0을 리턴해서 최대길이를 늘리지않는다
}
}
mid = (start+end)/2;
if(lis[mid] < target){
start = mid;
}
else{
end = mid;
}
}
return 0; // 사실 while내에서 함수가 종료되기때문에 이값은 의미가 없다.
}
위 알고리즘에서 lis_lowerbound 내의 for문의 i가 아래 그림에서의 i이며 한 번 for문을 수행 할 때마다 변화하는 lis[] 배열의 형태를 보여준다.

여기서 주의할 점은 이 알고리즘이 끝난 후 lis 배열의 원소개수가 최대증가수열 값을 의미하는 것이며, 그 배열 자체가 최대증가수열을 의미하지 않는다는 것이다.